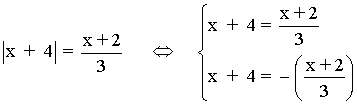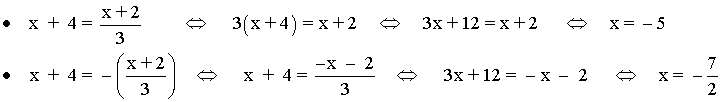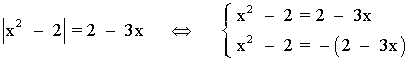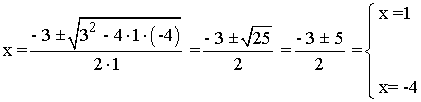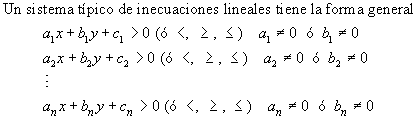Inecuaciones con valor absoluto.

Inecuaciones con valor absoluto.

Definición: Es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad. Si la desigualdad es del tipo < o > se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥  se denomina inecuación en sentido amplio.

  1)│ X │ < a < X < a (también se cumple para ≤). Se puede decir que la desigualdad queda dividida en dos partes : En la primera se “elimina” el módulo de valor absoluto y se mantiene lo demás igual (X < a), y en la segunda se “elimina” el módulo de valor absoluto, se cambia el sentido de la desigualdad y el signo del miembro de la derecha ( X > -a ), la solución viene dada por la INTERSECCIÓN de las dos soluciones parciales.

 2)│ X │ > aX > a U X < - a (también se cumple para ≥). Se puede decir que la desigualdad queda dividida en dos partes : En la primera se “elimina” el módulo de valor absoluto y se mantiene lo demás igual (X > a), y en la segunda se “elimina” el módulo de valor absoluto, se cambia el sentido de la desigualdad y el signo del miembro de la derecha ( X < - a ), la solución viene dada por la UNIÓN de las dos soluciones parciales. 

3) │X │ < │a │ X 2 < a 2 (también se cumple para >, ≥ y ≤). La solución se encuentra aplicando los métodos de resolución de una inecuación cuadrática o de segundo grado. 

4)│ X │ < – a Representa al conjunto vacío (también se cumple para ≤) 

Para resolver esta inecuación con valor absoluto se divide la misma en dos partes (Propiedad 1) :

 La primera parte será la misma inecuación sin el módulo de valor absoluto (4X – 1 ≤ 3)

 y en la segunda se cambiará el sentido del signo de la desigualdad y el signo del segundo miembro (4X – 1 ≥ – 3) La solución total será la INTERSECCIÓN de las dos soluciones parciales (Propiedad

Ejercicios:

∣ 3 - 4 x ∣ - 9 ≥ 0 ∣ 3 - 4 x ∣ - 9 + 9 ≥ 0 + 9 ∣ 3 - 4 x ∣ ≥ 9

∣ 3 - 4 x ∣ = 9

3 - 4 x = - 9 3 - 4 x - 3 = - 9 - 3 - 4 x = - 12 - 4 x - 4= - 12 - 4 x = 3

3 - 4 x = 9 3 - 4 x - 3 = 9 - 3 - 4 x = 6 - 4 x - 4 =6 - 4 x = - 3 2

∣ x - 20 ∣ = 6

x - 20 = - 6 x - 20 + 20 = - 6 + 20 x = 14

x - 20 = 6 x - 20 + 20 = 6 + 20 x = 26

x 14 ≤ x ≤ 26

IMÁGENES:

VIDEOS:

LINKS:

http://www.guiamath.net/ejercicios_resueltos/01_01_08_05-Inec_valor_abs_basicas/desarrollo_001.htm

http://www.monografias.com/trabajos-pdf4/inecuaciones-valor-absoluto/inecuaciones-valor-absoluto.pdf

http://es.slideshare.net/19671966/inecuaciones-convalorabsoluto3

http://brainly.lat/tarea/1302614

Ecuaciones cuadráticas con valor absoluto.

Una ecuación con valor absoluto se resuelve planteando dos ecuaciones resultantes de aplicar la definición de valor absoluto, el conjunto solución será un conjunto formado por dos elementos que satisfacen a la ecuación.

¿Cómo resolver una ecuación con Valor Absoluto?

Resolver una ecuación es encontrar un valor numérico que permita cumplir la igualdad. Cuando esta definición se suma con la definición de valor absoluto, se tendrán entonces dos valores que cumplan con ambas definiciones: Valor Absoluto: siempre valor positivo; ecuación: cumplir con la igualdad.

Los Objetivos de este artículo:

1) Mostrar como resolver una ecuación sencilla con valor absoluto

2) Como representar la solución, dos formas. Una analítica y otra en forma de conjunto.

El procedimiento es similar al de las ecuaciones lineales con la diferencia que en este caso las ecuaciones que resultan son cuadráticas y para resolverlas es necesario factorizarlas o utilizar la fórmula cuadrática.

Hallar el valor de x:

x 2 - 9 = x + 3

x 2 - 9 = x + 3		x 2 - 9 = - x + 3
x 2 - x - 1 2 = 0		x 2 - 9 = - x - 3
x - 4 x + 3 = 0		x 2 + x - 6 = 0
x = 4 x = - 3		x + 3 x - 2 = 0
		x = 2 x = - 3

Resolviendo cada ecuación, tenemos que: x=4, x=-3 y x=2

Reemplazando cada valor de x en la ecuación original tenemos:

EJERCICIOS:
6)   x + |1 + 2x| = - 2 Ambas soluciones cumplen la ecuación, por tanto: S = { -1 , 1} 7)   3|x + 4| - 2 = x Al comprobar las soluciones se observa que no cumplen la ecuación. Por tanto, la ecuación no tiene solución. 8)   |x2 - 2| = 2 - 3x Por otro lado, tenemos dos posibilidades para la igualdad:         •   x2 - 2 = 2 - 3x    ⇔    x2 + 3x - 4 = 0                 •   x2 - 2 = - (2 - 3x) = - 2 + 3x    ⇔    x2 - 3x = 0   ⇔   x ( x - 3) = 0             Comprobamos si las soluciones cumplen la ecuación: x = 1:      |12 - 2| = 2 - 3·1   ⇔   1 ≠ -1        x = 1 no es solución Hacemos lo mismo para el resto de soluciones. x = - 4 es solución x = 0 es solución x = 3 no es solución Por tanto, el conjunto solución es:             S = { -4 , 0 } 9)   |x + 1| = |x - 5| Se comprueba la solución x = 2 y la cumple la ecuación. x = 2 Tenemos dos posibilidades:      Por tanto, el conjunto solución es:                                          IMÁGENES:               VIDEOS: LINKS: http://laprofematematica.com/blog/ecuacion-con-valor-absoluto/ http://matematicatuya.com/DESIGUALDADES/S8_Ecuaciones_Absoluto.html http://www.analyzemath.com/spanish/Equations/Absolute_Value_Tutorial.html

Inecuaciones cuadráticas con 2 variables.

1. Vamos a estudiar ahora inecuaciones con dos incógnitas (x e y), en este caso al graficar la solución, en lugar de hacerlo en un sistema de ejes cartesianos, es decir se graficará en el plano.
2. Una inecuación con dos incógnitas, determina una región del plano, (de hecho inclusive una inecuación con una incógnita también puede determinar una región del plano, como veremos más adelante).
3. Vamos a resolver este tipo de inecuaciones en forma gráfica. Tomemos por ejemplo:

x + y ≤ 4

Como podemos ver, la suma de x + y debe ser siempre menor o igual a 4, y por supuesto hay infinitos pares de valores (x ,y) que cumplen la desigualdad.

Para determinar estos valores (que conformaran la región del plano que marcaremos como solución) dividiremos el problema en dos partes.

Primero determinaremos la recta que es el "límite" entre la región solución y la que no lo es.

Y luego que tenemos la recta, solo nos resta determinar de que "lado" de ésta se encuentra la solución.

Hechas estas aclaraciones, veamos el procedimiento:

x + y ≤ 4

x + y = 4 ⇒ y = 4 - x

Si x = 0 ⇒ y = 4 - 0 ⇒ y = 4

(Recomiendo elegir siempre x= 0 para el primer punto)

Si x = 4 ⇒ y = 4 - 4 ⇒ y = 0

Pocedimiento para trazar la gráfica del conjunto solución de una inecuación lineal

1.  Se traza la recta de la ecuación  ax + by + c = 0 2.  Se toma un punto de cada uno de los semiplanos determinados por la recta y se comprueba si verifican la inecuación dada 3.  Se sombrea el semiplano correspondiente al punto donde se verifica la inecuación.

Ejercicios:

             

   Ejercicio 2:

Paso 1: Reemplazando el signo de desigualdad por el signo =, obtenemos la siguiente ecuación :

$$

$$

$x$ + y = 4 . Para graficar una recta, es suficiente hallar dos puntos. Una forma sencilla de graficar la recta es hallar los interceptos con los ejes: 

Para hallar el intercepto con el eje x, hacemos y=0, 

$x+\mathrm{y}$ = 4 x+ 0 = 4 x = 4

Para hallar el intercepto con el eje y, hacemos x=0, 

$x$ + y = 4 0 + y = 4 y = 4

La gráfica de la recta es la siguiente. Esta recta divide el plano en dos regiones R1 y R2.

Ejemplo 3:

Resolver la siguiente inecuación $2$ x + 3 y ≥ 6

Paso 1: Reemplazando el signo de desigualdad por el signo =, obtenemos la siguiente ecuación
$2$ x + 3 y = 6 . Para graficar una recta, es suficiente hallar dos puntos. Una forma sencilla de graficar la recta es hallar los interceptos con los ejes:
Para hallar el intercepto con el eje x, hacemos y=0, 

$\begin{array}{c}2\end{array}$ x + 3 y = 6 2 x + 3 ( 0 ) = 6 2 x = 6 x = 3

Para hallar el intercepto con el eje y, hacemos x=0, 

$\begin{array}{c}2\end{array}$ x + 3 y = 6 2 ( 0 ) + 3 y = 6 y = 2

La gráfica de la recta es la siguiente. Esta recta divide el plano en dos regiones R1 y R2.

Paso 2: Tomar puntos de prueba en cada región y verificar si satisfacen la desigualdad.
Punto de prueba en R1 (1,1) $2$ x + 3 y ≥ 6 2 ( 1 ) + 3 ( 1 ) ≥ 6 5 ≥6 Como la expresión es falsa, entonces esta región no es solución de la inecuación.	Punto de prueba en R2 (3,4) $2$ x + 3 y ≥ 6 2 ( 3 ) + 3 ( 4 ) ≥ 6 18 ≥ 6 Como la expresión es verdadera, entonces esta región es la solución de la inecuación.

Graficar la solución. Como el signo de desigualdad es ≥ se debe incluir la frontera como parte de la solución. Para denotar este hecho gráficamente, utilizaremos una linea continua en la frontera.

Ejemplo 3:

Resolver la siguiente inecuación en dos dimensiones $x$ > 2


Paso 1: Reemplazando el signo de desigualdad por el signo =, obtenemos la siguiente ecuación
$x$ = 2 . Esta ecuación corresponde a una recta vertical con intercepto en el punto x=3. 

               

                

Paso 2: Tomar puntos de prueba en cada región y verificar si satisfacen la desigualdad.
Punto de prueba en R1 (0,0) $x$ > 2 0 > 2 Como la expresión es falsa, entonces esta región no es solución de la inecuación.	Punto de prueba en R2 (3,3) $x$ > 2 3 > 2 Como la expresión es verdadera, entonces esta región es la solución de la inecuación.
Paso 2: Graficar la solución. Como el signo de desigualdad es > no se debe incluir la frontera como parte de la solución.

                 

Imágenes:

VIDEOS:

LINKS:

http://www.vitutor.com/ecuaciones/ine/ine2_Contenidos.html

http://www.vadenumeros.es/primero/graficas-de-inecuaciones.htm

https://www.youtube.com/watch?v=SCe08paMyLY