Matemática 1BGU ·1·: Inecuaciones cuadráticas con 2 variables.

Vamos a estudiar ahora inecuaciones con dos incógnitas (x e y), en este caso al graficar la solución, en lugar de hacerlo en un sistema de ejes cartesianos, es decir se graficará en el plano.
Una inecuación con dos incógnitas, determina una región del plano, (de hecho inclusive una inecuación con una incógnita también puede determinar una región del plano, como veremos más adelante).
Vamos a resolver este tipo de inecuaciones en forma gráfica. Tomemos por ejemplo:

x + y ≤ 4

Como podemos ver, la suma de x + y debe ser siempre menor o igual a 4, y por supuesto hay infinitos pares de valores (x ,y) que cumplen la desigualdad.

Para determinar estos valores (que conformaran la región del plano que marcaremos como solución) dividiremos el problema en dos partes.

Primero determinaremos la recta que es el "límite" entre la región solución y la que no lo es.

Y luego que tenemos la recta, solo nos resta determinar de que "lado" de ésta se encuentra la solución.

Hechas estas aclaraciones, veamos el procedimiento:

x + y ≤ 4

x + y = 4 ⇒ y = 4 - x

Si x = 0 ⇒ y = 4 - 0 ⇒ y = 4

(Recomiendo elegir siempre x= 0 para el primer punto)

Si x = 4 ⇒ y = 4 - 4 ⇒ y = 0

Pocedimiento para trazar la gráfica del conjunto solución de una inecuación lineal

1. Se traza la recta de la ecuación ax + by + c = 0

2. Se toma un punto de cada uno de los semiplanos determinados por la recta y se comprueba si verifican la inecuación dada

3. Se sombrea el semiplano correspondiente al punto donde se verifica la inecuación.

Ejercicios:

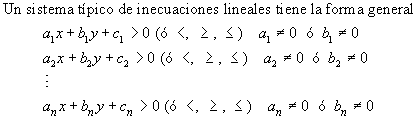
Ejercicio 2:

Paso 1: Reemplazando el signo de desigualdad por el signo =, obtenemos la siguiente ecuación :

$x$ + y = 4 . Para graficar una recta, es suficiente hallar dos puntos. Una forma sencilla de graficar la recta es hallar los interceptos con los ejes:

Para hallar el intercepto con el eje x, hacemos y=0,

$x + y$ = 4 x+ 0 = 4 x = 4

Para hallar el intercepto con el eje y, hacemos x=0,

$x$ + y = 4 0 + y = 4 y = 4

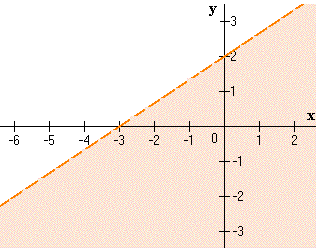
La gráfica de la recta es la siguiente. Esta recta divide el plano en dos regiones R1 y R2.

Ejemplo 3:

Resolver la siguiente inecuación $2$ x + 3 y ≥ 6

Paso 1: Reemplazando el signo de desigualdad por el signo =, obtenemos la siguiente ecuación
$2$ x + 3 y = 6 . Para graficar una recta, es suficiente hallar dos puntos. Una forma sencilla de graficar la recta es hallar los interceptos con los ejes:
Para hallar el intercepto con el eje x, hacemos y=0,

$\begin{matrix} 2 \end{matrix}$ x + 3 y = 6 2 x + 3 ( 0 ) = 6 2 x = 6 x = 3

Para hallar el intercepto con el eje y, hacemos x=0,

$\begin{matrix} 2 \end{matrix}$ x + 3 y = 6 2 ( 0 ) + 3 y = 6 y = 2

La gráfica de la recta es la siguiente. Esta recta divide el plano en dos regiones R1 y R2.

Paso 2: Tomar puntos de prueba en cada región y verificar si satisfacen la desigualdad.
Punto de prueba en R1 (1,1) $2$ x + 3 y ≥ 6 2 ( 1 ) + 3 ( 1 ) ≥ 6 5 ≥6 Como la expresión es falsa, entonces esta región no es solución de la inecuación.	Punto de prueba en R2 (3,4) $2$ x + 3 y ≥ 6 2 ( 3 ) + 3 ( 4 ) ≥ 6 18 ≥ 6 Como la expresión es verdadera, entonces esta región es la solución de la inecuación.

Graficar la solución. Como el signo de desigualdad es ≥ se debe incluir la frontera como parte de la solución. Para denotar este hecho gráficamente, utilizaremos una linea continua en la frontera.

Ejemplo 3:

Resolver la siguiente inecuación en dos dimensiones $x$ > 2

Paso 1: Reemplazando el signo de desigualdad por el signo =, obtenemos la siguiente ecuación
$x$ = 2 . Esta ecuación corresponde a una recta vertical con intercepto en el punto x=3.

Paso 2: Tomar puntos de prueba en cada región y verificar si satisfacen la desigualdad.
Punto de prueba en R1 (0,0) $x$ > 2 0 > 2 Como la expresión es falsa, entonces esta región no es solución de la inecuación.	Punto de prueba en R2 (3,3) $x$ > 2 3 > 2 Como la expresión es verdadera, entonces esta región es la solución de la inecuación.
Paso 2: Graficar la solución. Como el signo de desigualdad es > no se debe incluir la frontera como parte de la solución.