Introducción:
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que comparten dos o más incógnitas. Las soluciones de un sistema de ecuaciones son todos los valores que son válidos para todas las ecuaciones, o los puntos donde las gráficas de las ecuaciones se intersectan.
Podemos resolver un sistema de ecuaciones lineales graficando, por sustitución y por combinación lineal. Los sistemas de funciones no lineales, como ecuaciones cuadráticas o exponenciales, pueden ser manejados con las mismas técnicas.
Empecemos por hablar sobre dos ecuaciones lineales.
Si las gráficas de las ecuaciones se intersectan, entonces existe una solución para ambas ecuaciones.
|
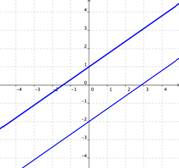
Si las gráficas de dos ecuaciones no se intersectan (por ejemplo, si son paralelas), entonces no existen soluciones para ambas ecuaciones.
|
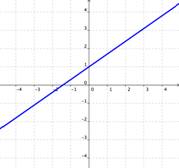
Si las gráficas de las ecuaciones son la misma, entonces hay un número infinito de soluciones para ambas ecuaciones.
|
Para resolver un sistema con una ecuación lineal y una ecuación cuadrática, podemos hacer lo mismo, encontrar el punto de intersección entre gráficas.
Una solución
|
No hay solución
|
Soluciones infinitas
|
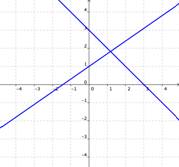 |  |  |
Si las gráficas de las ecuaciones se intersectan, entonces existe una solución para ambas ecuaciones.
|
Si las gráficas de dos ecuaciones no se intersectan (por ejemplo, si son paralelas), entonces no existen soluciones para ambas ecuaciones.
|
Si las gráficas de las ecuaciones son la misma, entonces hay un número infinito de soluciones para ambas ecuaciones.
|
Para resolver un sistema con una ecuación lineal y una ecuación cuadrática, podemos hacer lo mismo.
Una solución No hay solución Dos soluciones
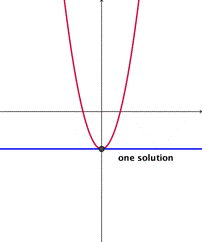
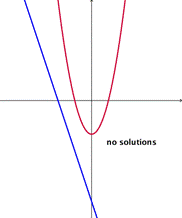
Si la parábola y la recta se tocan en un sólo punto, entonces existe una solución para ambas ecuaciones.
|
Si las gráficas de las ecuaciones no se intersectan, entonces no existen soluciones para ambas ecuaciones.
|
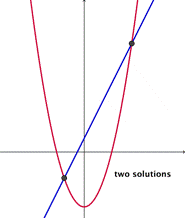
Si la recta se intersecta con la parábola en dos lugares, entonces hay dos soluciones para ambas ecuaciones.
|
Ejercicios:
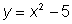
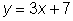
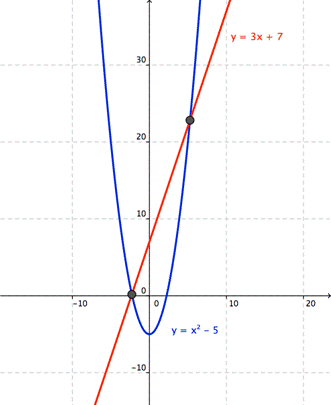
Graficar cada ecuación y localizar los puntos de intersección.
Este sistema tiene dos soluciones, No podemos determinar la posición exacta de los puntos de intersección a partir de la gráfica, pero son aproximadamente (-2,0) y (5,22).
Ahora vamos a resolver el mismo sistema usando sustitución.
- Seleccionar una ecuación y despejar una variable. (Escoger una ecuación y una variable que sea fácil de despejar).
- Sustituir la expresión resultante por una variable en la otra ecuación, cada vez que esta variable aparezca.
- Resolver la segunda variable en la segunda ecuación.
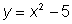
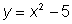
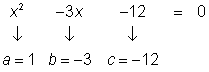
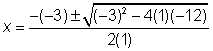
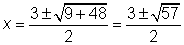
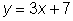
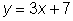
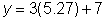

(5.27, 22.82) y (-2.27, 0.18)
Podemos resolver el sistema de ecuaciones cuadráticas graficando:
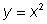 y
y 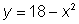
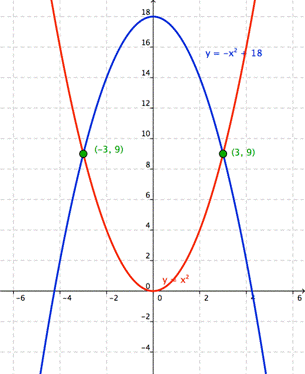
Solución:
(-3, 9) y (3, 9)
Ejercicio:
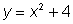 y
y 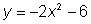
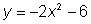
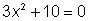
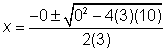
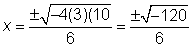
No hay solución.
Imágenes:
VIDEOS:
LINKS:








No hay comentarios.:
Publicar un comentario