Una ecuación con valor absoluto se resuelve planteando dos ecuaciones resultantes de aplicar la definición de valor absoluto, el conjunto solución será un conjunto formado por dos elementos que satisfacen a la ecuación.
¿Cómo resolver una ecuación con Valor Absoluto?
Resolver una ecuación es encontrar un valor numérico que permita cumplir la igualdad. Cuando esta definición se suma con la definición de valor absoluto, se tendrán entonces dos valores que cumplan con ambas definiciones: Valor Absoluto: siempre valor positivo; ecuación: cumplir con la igualdad.
Los Objetivos de este artículo:
1) Mostrar como resolver una ecuación sencilla con valor absoluto
2) Como representar la solución, dos formas. Una analítica y otra en forma de conjunto.
El procedimiento es similar al de las ecuaciones lineales con la diferencia que en este caso las ecuaciones que resultan son cuadráticas y para resolverlas es necesario factorizarlas o utilizar la fórmula cuadrática.
Hallar el valor de x :
Resolviendo cada ecuación, tenemos que: x = 4 x = - 3 x = 2
Reemplazando cada valor de x en la ecuación original tenemos:
| EJERCICIOS: | ||
6) x + |1 + 2x| = - 2
Ambas soluciones cumplen la ecuación, por tanto:
S = { -1 , 1}
7) 3|x + 4| - 2 = x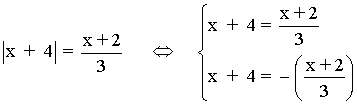 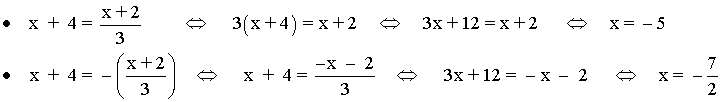
Al comprobar las soluciones se observa que no cumplen la ecuación.
Por tanto, la ecuación no tiene solución.
8) |x2 - 2| = 2 - 3x
Por otro lado, tenemos dos posibilidades para la igualdad:
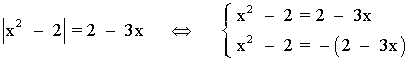
• x2 - 2 = 2 - 3x ⇔ x2 + 3x - 4 = 0
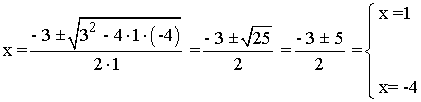
• x2 - 2 = - (2 - 3x) = - 2 + 3x ⇔ x2 - 3x = 0 ⇔ x ( x - 3) = 0
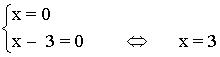
Comprobamos si las soluciones cumplen la ecuación:
x = 1: |12 - 2| = 2 - 3·1 ⇔ 1 ≠ -1 x = 1 no es solución
Hacemos lo mismo para el resto de soluciones.
x = - 4 es solución
x = 0 es solución
x = 3 no es solución
Por tanto, el conjunto solución es:
S = { -4 , 0 }
9) |x + 1| = |x - 5|
Se comprueba la solución x = 2 y la cumple la ecuación.
x = 2
|
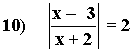
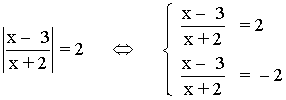
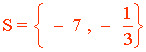





No hay comentarios.:
Publicar un comentario