Funciones cuadráticas.
Las funciones cuadráticas son funciones polinómicas es
de segundo grado, siendo su gráfica una parábola.
Podemos resolver cualquier ecuación
cuadrática completando el cuadrado — convirtiendo un polinomio
en un trinomio cuadrado perfecto.
Si completamos el cuadrado en la ecuación
genérica y luego resolvemos x,
encontramos que:
f(x) = ax2 + bx + c
1.- ax2 es el término cuadrático2.-bx es el término lineal 3.-c es el término independiente
· Empezar con una
ecuación de la forma x² + bx +c = 0.
· Reescribir la
ecuación de forma que x² + bx quede despejada.
· Completar el cuadrado sumando (b/2)² a ambos lados.
· Reescribir como el
cuadrado de un binomio y resolver x.
Solución por factorización
En toda ecuación cuadrática uno de sus miembros es un
polinomio de segundo grado y el otro es cero; entonces, cuando el polinomio de
segundo grado pueda factorizar, tenemos que convertirlo en un producto de
binomios.
Obtenido el producto de binomios, debemos buscar el valor de x de
cada uno.
Para hacerlo igualamos a cero cada factor y se despeja para la variable.
Igualamos a cero ya que sabemos que si un producto es igual a cero, uno de sus
multiplicandos, o ambos, es igual a cero.
Ejemplos:
1) Resolver
(x + 3)(2x − 1) = 9
Lo primero es igualar la ecuación a cero.
Para hacerlo, multiplicamos los binomios:
Ahora, pasamos el 9, con signo contrario, al primer miembro para igualar a cero:
Ahora podemos factorizar esta ecuación:
(2x − 3)(x + 4) = 0
Ahora podemos igualar a cero cada término del producto para resolver las incógnitas:
Si
2x − 3 = 0
2x = 3
Si
x + 4 = 0
x = −4
2)Resolver con función cuadráticas.
x2 – 6x = − 8
x2 – 6x = −8 /+9 (sumamos 9 en ambos miembros de la ecuación)
x2 − 6x + 9 = − 8 + 9
(x – 3)2 = 1
Extraemos las raíces cuadradas
y queda
x – 3 = 1 y x − 3 = −1
Si
x – 3 = 1
x = 1 + 3
x = 4
Si
x – 3 = −1
x = −1 + 3
x = 2
Por lo tanto x1 = 4 y x2 = 2
3)Resolver.
2x2 + 3x − 5 = 0
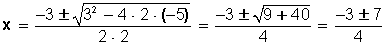
x:1 x:-2.5
Algunos ejemplos, con soluciones
1) Resolver: − 5x2 + 13x + 6 = 0
Se identifican las letras, cuidando que la ecuación esté ordenada respecto a la x, de grado mayor a menor. Con esta condición tenemos: a = − 5; b = 13; c = 6.
Se aplica la fórmula:
Como la raíz buscada es 17 (el cuadrado de 17 es 289), se tiene entonces que:
Según esto, tendremos dos raíces diferentes, una usando el signo + y otra usando el signo
Llamaremos X1 y X2 a las dos soluciones, que serán:
IMÁGENES:
VIDEOS:
LINKS:



No hay comentarios.:
Publicar un comentario